Archivo por meses: junio 2018

Introducción a la tomografía fotoacústica

Uncategorized

La Tomografía Fotoacústica (PAT – por sus siglas en inglés) es una modalidad de imagen médica que combina las ondas ópticas con las ondas acústicas para obtener imágenes del interior de un cuerpo. En los últimos años se ha explorado la idea de combinar distintas ondas para obtener las mejores características diagnósticas de cada onda. En términos generales, las imágenes que se obtienen de usar solamente ondas ópticas están caracterizadas por tener un alto contraste pero una baja resolución, mientras que las que se obtienen de ondas acústicas se caracterizan por una alta resolución pero un bajo contraste. La idea de estas modalidades es hacer un acoplamiento físico de las ondas para obtener las mejores propiedades de cada una. A estas modalidades se le conocen como métodos de ondas múltiples o acopladas en la comunidad de biomedicina y como problemas inversos híbridos o acoplados en la comunidad matemática. PAT es uno de estos métodos que ha despertado el interés de distintas comunidades por sus potenciales aplicaciones, bajo costo y complejidad matemática. En este video el profesor Lihong Wang de la Universidad de Washington St. Louis habla de aplicaciones de PAT.

Cuando cortos pulsos de ondas electromagnéticas se usan para irradiar un tejido biológico, el efecto fotoacústico/termoacústico resulta en la emisión de señales acústicas («el sonido de la luz»). En este video se ilustra el efecto termoacústico. Estas ondas acústicas se miden en el exterior del objeto por medio de transductores ultrasónicos de banda ancha y esta información se utiliza para obtener el coeficiente de difusión del tejido. El proceso se ilustra en la siguiente Figura 1.

pat
Fig. 1. Proceso de acoplamiento de ondas en tomografía acústica

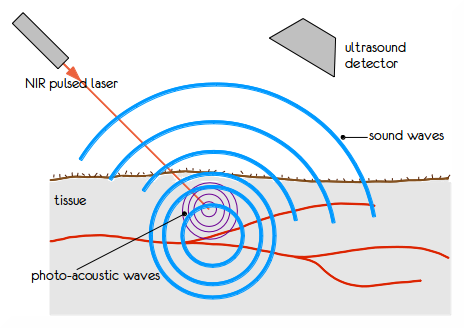
Dicho en otras palabras, el objetivo principal de la PAT es obtener información del coeficiente de absorción electromagnético del tejido utilizando las mediciones acústicas producidas por el efecto fotoacústico. La información del coeficiente de absorción está relacionado con la estructura molecular del tejido y una buena reconstrucción de este puede revelar condiciones patológicas que facilite el diagnóstico de enfermedades (e.g., cancer de piel o de mama). A continuación presentamos una descripción matemática de PAT, brevemente mencionando las razones físicas detrás de esta modalidad.

El proceso de PAT se divide en dos partes. La primera consiste en utilizar las mediciones acústicas para recuperar información interna de la radiación absorbida por el tejido. Este proceso se modela como la reconstrucción de la condición inicial en la ecuación de onda utilizando información lateral. Sea {\Omega} un dominio acotado con frontera suave y suponga que {\Omega} se puede extender infinitamente sin perturbar las mediciones, entonces la presión acústica {p} satisface la ecuación de onda,

\displaystyle \begin{array}{rclr} \frac{1}{c^2(x)} \partial_t^2p - \Delta p &= &0, & (t,x)\in(0,\infty)\times {\mathbb R},\\ p(0,x) &=& H(x), & x\in {\mathbb R},\\ \partial_tp(0,x) &=& 0, & x\in {\mathbb R}, \end{array} \ \ \ \ \ (1)

donde {c(x)\in C_c^\infty(\Omega)} es la velocidad de la onda y {H(x)\in H_0^1(\Omega)} es la señal ultrasónica generada tiempo {t=0}. Entonces el primer paso consiste en recuperar

\displaystyle (H,c) \quad \mbox{usando} \quad p(t,x)|_{(0, T)\times \partial \Omega} \ \ \ \ \ (2)

para algún tiempo finito {T >0}.
Note que el efecto de la propagación de radiación está modelado como una condición inicial a tiempo {t=0}. La justificación detrás es la gran diferencia entre las velocidad de la luz (aprox. {2.3\times 10^8 m/s}) y la del sonido (aprox. {1.5 \times 10^3 m/s}), desde el punto de vista de la onda acústica toda la radiación electromagnética sucede a tiempo cero. Esta suposición es robusta pues en el caso de PAT los fotones están cerca del espectro infrarrojo con longitudes de onda entre {600nm} y {900nm}. Finalmente, como la dependencia de {H} de las mediciones {p(t,x)|_{(0, T)\times \partial \Omega}} es lineal, decimos que la recuperación de {H} es un problema inverso lineal (en contraste, recuperar {c} es un problema inverso no lineal).

El segundo paso en PAT se conoce como Tomografía Fotoacústica Cualitativa (qPAT-por sus siglas en inglés) y el objetivo principal es obtener propiedades electromagnéticas del tejido por medio de la medición interna {H} obtenida en el primer paso y la iluminación inicial. La radiación electromagnética se modela típicamente por medio de la ecuación de difusión o por la ecuación de transporte. Aquí usaremos la formulación difusiva que modela la densidad espacial del photon {u} por medio de la ecuación elíptica con condición de frontera de Dirichlet dada por,

\displaystyle \begin{array}{rcr} -\nabla\cdot \gamma(x) \nabla u + \sigma(x)u = 0 & \mbox{en}& \Omega,\\ u=f & \mbox{sobre} & \partial \Omega, \end{array}, \ \ \ \ \ (3)

donde {\gamma(x)} es el coeficiente de difusión y {\sigma(x)} el coeficiente de absorción que asumimos son funciones con valores complejos y tales que {0<\epsilon < \gamma, \sigma < \frac{1}{\epsilon}} para {\epsilon>0}. En la ecuación (3), {f(x)} es la iluminación inicial usada para probar el tejido biológico y {H} es el coeficiente interno obtenido en el primer paso y es igual a

\displaystyle H(x) = \Gamma(x)\sigma(x)u(x) \quad x \in \Omega, \ \ \ \ \ (4)

donde {\Gamma(x)} es el parámetro de Güneisen (que modela la fuerza del efecto fotoacústico). De esta manera el objetivo de qPAT es reconstruir

\displaystyle (\gamma, \sigma, \Gamma) \quad \mbox{utilizando} \quad (H,f).

En resumen, por medio de estos dos pasos convertimos la información acústica {p(t,x)|_{(0, T)\times \partial \Omega}} en información del coeficiente de absorción {\sigma}. Para mayor información de la matemáticas de PAT se pueden consultar los siguientes artículos resumen

  • Multi-wave methods via ultrasound, P. Stefanov y G. Uhlmann, Inside Out II, MSRI publications, Cambridge University Press, 2012
  • Mathematical Methods in Photoacoustic imaging, O. Scherzer y P. Kuchment, Encyclopedia of Applied and Computational Mathematics, Springer Verlag 2015.
  • Hybrid inverse problems and internal functionals G. Bal y G. Uhlmann, Inside Out II, MSRI Publications, Cambridge University Press, 2012